Scratch融入負數與數線教學
前言:
由電腦解題—數學篇。
為什麼選數學,是因為電腦根本是數學的翻版,所以先由數學著手。
早在好幾年前,就有想過要用電腦的程式設計來輔助數學教學,原因如下:
1.程式設計是利用電腦解決人類所遇到問題,這點剛好跟數學的理念相同。
2.程式設計沒有標準程式碼,這點跟數學的一題多解理念相同。
3.程式設計有基本語法需遵守,這點跟數學需要遵守的基本觀念理念相同。
4.程式設計有演算法,這點跟數學的式理念相同。
受限於當時軟、硬體的限制,一直沒辦法找到好的方法可以教導小朋友程式設計的概念。
不要說小朋友,連大人聽到 程式設計 四個字,也都退避三舍。
直到,2107年初,無意間得知教改新課綱要納入資訊科技,在好奇心的驅使下,產開一系列的爆肝之旅。
了解未來新趨勢:
第一步,先來去教育部了解,何謂107年課綱
http://www.naer.edu.tw/files/15-1000-7944,c639-1.php?Lang=zh-tw
教育部網站,寫得都是中文,很詳細,有興趣的可以仔細閱讀。
整理了一下,節錄內容如下:
107年課綱:由「國家教育研究院」規劃的107課綱草案,
預計新政府上路後,教育部將會重組「課審會」進行審議。
根據既定草案內容,「程式設計」將屬於科技領域的一部分,
國中、高中階段列為必修課程,但在
國小階段,則可依照學校資源條件與學生特性,
進行融入性的教學規劃,或是也可成立社團提供學生學習。
第二步,原來一年前,我兒子玩的那個學校迷宮遊戲,還有全省跟全台中市排名的,用的是Scratch的設計軟體,跟印象中樂高的NXT使用的介面很像,都是用積木排來排去。
那就來了解一下,什麼是Scratch ?
美國麻省理工學院開發了一套兒童程式語言【Scratch】,
特色在於沒有複雜的文字指令,
所有的指令都是以視覺化的積木來呈現。
要完成一個程式,只要像組合積木一樣,
就可以完成一個程式。
因此,完全沒有程式設計經驗的孩子可以立刻上手,
開始設計程式。
Scratch官網
Code.Org
原來是一套行之有年的程式設計軟體,之前是1.4版,現在大改版到2.0版。
其實還有其他的設計軟體可以選擇,例如KUDO,可是既然學校教的是Scratch,還是以Scratch為主吧!
第三步,繼續查資料,發覺Scratch跟Arduino好像有極大的關聯性,好奇心再次驅使,便去了解了一下。
維基百科的介紹,開放原始碼的單晶片微控制器,看到開放原始碼,眼晴馬上亮了起來。
https://zh.wikipedia.org/wiki/Arduino
第四步,當時正好為中台灣空污最嚴重之時,不能出門運動,就想在家動手做,當時就興起來做個隨身型PM2.5空氣盒子,二話不說,工程師模式啟動,馬上行動。
開發板、電源板、顯示裝置、麵包板、電源盒、感測器,所有硬體備齊,開始接線,硬體接線實非我所長,所以過程中,自己也燒壞了一片開發板,然而一切的關鍵,還是屬於軟體設計的部份。
好險,軟體設計對我而言不會困難,而且Arduino是屬於簡單的C語言架構,參考一下資料,再自行研讀一下資料,上手並不難,當然也要感謝那段期間幫助過我的朋友們。
可以自行參考
http://jaihung.blogspot.com/2017/02/pm2.5arduino.html
第五步,要把成品放在一個保護良好的外殼中,市面上找不到合適的,只好另找出路,結果找到的解決方法是,自己做,因此,3D列印又成了最好的選擇。
找好開源碼的3D列印,又需要建模軟體,又是一個不是我專精的領域,求助他人又碰壁,好險現在網路資源發達,建模軟體也有免費或者是教育版本,還有雲端版本,不用像以前一樣,為了建模,要去買一台高階電腦回來用,真的是很方便。
第六步,自行摸索了一次,覺得這些真的是未來的趨勢,因此回過頭來規劃國中小的教學版本,總共設計出了三大主題,八大課程。
課程規劃:
使用將Scratch融入STEAM教學,將電腦當成教學輔助工具來使用,一方面可以豐富課程內容,一方面又可以提升學習興趣。
提供開發程式所需的流程步驟,按步就班,可以大幅滅少備課時間。
開發程式的關鍵在於是否能於有限的資源中,解決所面臨的問題,正確的程式設計觀念極其重要。
因屬於融入性課程,所以時間非常彈性,可以依照需求,自行調整。
本單元的教學步驟
電腦本身就是一個設計用來解決人類問題的工具,除了學習數學負數與數線的教學目標之外,還需要具備電腦程式設計的基礎,才能達成融入教學的目的。在本次單元課程中,將會學到:
一、
負數與數線:
1.
認識負數
2.
加法和減法
3.
乘法和除法
4.
數的四則運算
5.
數線
二、
電腦程式設計概念:
1.
下載和安裝
2.
設定環境
3.
基本操作和概念
4.
程式設計流程
5.
技巧和互動
6.
測試和除錯
(有些格式顯示不出來,請見諒)
負數與數線
² 認識負數
學習目標
s 能以「正、負」表徵生活中相對的量,並且認識負數是性質(方向、高度、溫度等)的相反。
s 能認識絕對值符號跟定義。
s 能運算絕對值。
s 能比較數的大小(包括負數)。
課程教案
附註
|
學習評估
|
課程
|
時間
|
認識負數-負數、相反數、負負得正、絕對值和數的比較大小。
|
|||
溫度、海拔。
|
正數是大於0的數,負數是小於0的數。
給一個正數a,就有一個負數-a。
|
「負數是小於0的數」是學習負數的第一個概念。
|
|
-(8-6)=-2
|
理解同一負數可能有不同型式,但其值是一樣的性質。
|
||
相反數。
|
|||
賺錢賠錢,東邊西邊。
|
記錄一些彼此相反或相對的量。
|
相反的性質可用正、負數表示,在正負數的應用相當重要。
|
|
水結冰的溫度、海平面的定義。
|
中午12點為基準跟下午2點為基準表示有何不同?
|
用正負數來描述相概念,務必包含「基準」與「正向」的約定。
|
|
相反數的定義。
-5和-(-5)為相反數。
|
不論a是0、正數或負數,a和-a互為相反數。
|
||
a=-(-a);
-(-a)=a。
|
學習用a=負數,代入-(-a)=a的公式。
|
||
絕對值。
|
|||
大於或等於0的數。
|
絕對值的定義。
|
||
-(-a)=a,-
|
分辨-(-a)與-
|
||
數的大小。
|
|||
比較兩個負數時,絕對值較大的數較小。
|
(1)從賺錢跟賠錢來比。
(2)從位置高度來比。
(3)從溫度來比。
|
||
² 加法和減法
學習目標
s 能判別兩數加減的正負結果並算出其值。
s 能理解負數的特性並熟練數(包括分數、小數)的加減運算。
附註
|
學習評估
|
課程
|
時間
|
加法和減法-學習負數的概念後,將加減運算推廣至包括負數的運算,可以更容易了解引入負數的好處及負數運算的合理性。
|
|||
賺500記為+500,賠500記為-500。
|
詳述並提醒注意負數與算式的連結,要能體會其關連性。
|
||
一般數的加法
|
|||
(-500)+750=750-500=250,
750+(-1000)=750-1000=-(1000-750)=-250,由上可得,若a和b為正數,可得。
|
加法的交換律。
加法的結合律。
a+(-b)=a-b。
|
||
a和b為正數。
|
(-a)+(-b)=-(a+b)。
|
||
一般數的減法
|
|||
a和b為正數。
|
(-a)-b=-(a+b)=(-a)+(-b)。
a-(-b)=a+b。
|
||
減去一個數相當於加它的相反數。
a-b=a+(-b)。
-(a+b)=-a-b。
|
|||
負負得正:-(-a)=a。
|
|||
小數減大數=-(大數減小數)。
a-b=-(b-a)。
|
加減規則中最重要的是:小的數減大的數,以及減一個數相當於加它的相反數。
|
||
透過觀察運算式的變化,理解(1)減一個數相當加上它的相反數,(2)加一個數相當減去它的相反數,由此可以處理「減數」為負的計算。
|
|||
去括號規則,如-(a+b)=-a-b,可以視為a+b的相反數等於-a-b或a+b相反數相加。
|
|||
公式-(a+b)=b-a可視為「a-b的相反數等於b-a」。
|
|||
² 乘法和除法
學習目標
s 能判別兩數乘除的正負結果並算出其值。
s 能熟練數(包括分數、小數)的乘除運算。
附註
|
學習評估
|
課程
|
時間
|
乘法和除法-將正數的乘除運算推廣至一般數(含負數)的乘除運算,正數的乘法交換律、結合律、分配律,也因此能推廣到一般數。
|
|||
做正負數相乘時,應先判斷乘積為正數或負數,然後將其餘的正數部份做運算。
|
|||
一般數的乘法
|
|||
(-a)×b=-(a×b)。
(-a)×(-b)=a×b。
|
|||
乘法負號也適用交換律。
|
乘法有交換律。
|
a×(-b)=-(a×b)。
|
|
兩數的正、負號相同,稱為同號。
兩數的正、負號不同,稱為異號。
|
性質符號和運算符號定義。
|
同號的兩數相乘,其值為正。
異號的兩數相乘,其值為負。
|
|
乘法的性質
|
|||
1乘以任何數a都等於a。
|
|||
1×3=3。
1×(-3)=-3。
(-1)×3=-3
(-1)×(-3)=3。
|
(-1)乘以a等於多少呢?
若a>0,其值為-a。
若a<0,其值為a。
|
||
(-1)×a=-a。
a的相反數可以寫成-a,
也可以寫成(-1)×a。
|
|||
乘法交換律。
乘法結合律。
|
|||
仿照說明的方式來做,並讓學習者說明過程。
|
說明乘法的交換律,過程中不把算式算出,用意在呈現其規則對一般數均成立。
|
||
學習以乘法對加法交換律逆向思考,藉以應用b×a+c×a=(b+c)×a的規則,並為將來因式分解的提公因式做鋪陳。
|
|||
倒數
|
|||
跟正數的倒數定義一樣。
|
求倒數要先將帶分數換成假分數,再求倒數。
|
||
負數的倒數還是負數。
|
|||
除以一個不為0的數等於乘上這個數的倒數。
|
沿用正數中「除以一個不為0的數等於乘上它的倒數」來約定負數的除法規則。
|
||
除法在一般數的定義是延續正數的做法。
|
|||
同號的兩數相除,其值為正。
異號的兩數相除,其值為負。
|
|||
提醒
|
|||
² 數的四則運算
學習目標
s 能熟練數(包括分數、小數)的四則運算規則。
附註
|
學習評估
|
課程
|
時間
|
含有負數的四則運算與正數並無不同。重點在於熟悉含負數的四則混和運算,並學習善用運血規則(交換律、結合律、分配律)以簡化計算。
|
|||
透過練習,選擇適當的方法來簡化計算。
|
|||
四則運算的規則
|
|||
再次強調:
減去一個數,等於加上這個數的相反數。
除以一個不為0的數,相當於乘以它的相反數。
|
算式中沒括號:
依照先乘除後加減,以及從左到右的順序的原則來做計算。
算式中有括號:
先算括號中的算式,有多重括號,要從最裏層的括號先算。
|
||
交換律、結合律、分配律的應用。
|
說明雖然依序相加或相乘都可以得到正確的答案,然而靈活運算規律可以簡化計算。
|
||
利用分配律先去括號,再作計算,有時,會比較簡單,學習去括號的好處。
|
|||
學習先觀察題目,再決定是否先去括號。
|
|||
² 數線
學習目標
s 能認識如4及-4在數線上的相對位置。
s 能在數線上判斷數的大小
s 能在數線上操作簡單的描點,如-4、(-3)+5、(-2)×3等,並介兩點在數線上的間隔。
s 能理解絕對值在數線上的圖義。
s 能用絕對值的符號表示數線上兩點間的間隔(距離)。
附註
|
學習評估
|
課程
|
時間
|
說明數線、距離跟絕對值的關係
|
|||
A(a):A點的坐標為a。
|
用一個數來標示某一點的位置,這個數就稱做這一點的坐標。
|
||
認識數線
|
|||
任意數b>0,把A(a)向右移b個單位後,所得的點坐標為a+b,向左移b個單位後,所得的點坐標為a-b。
|
點的判讀、在數線上描點、利用點的向左、向右移動來詮釋加減法運算的幾何。
|
||
特別說明,數線上「原點、單位長、方向和坐標」等約定的名詞。
|
|||
利用比出坐標的大小,來決定「點的左、右關係」
|
|||
能在數線上利用「點的位置」判讀「數的大小」。
|
|||
距離與絕對值
|
|||
以兩點座標差的絕對值來表示兩點間的距離。
|
|||
利用距離相等的想法來介紹兩點之間的中間坐標,來了解「幾何」與「代數」結合概念。
|
|||
A(a)到原點的距離
|
A(a)到原點的距離=
|
||
如果A(a)和B(b)是數線上兩點,則不管a>b或a<b,都有
|
|||
絕對值的幾何意義就是距離。
|
推導出數線上任意兩點的距離是兩點坐標的差,也就是A(a)和B(b)的距離=
|
||
可適時補充。
|
中點坐標公式。
|
||
電腦程式設計概念
課程前後順序可以互相調整,並不影響學習效果。
一、負數與數線。
二、Scratch 2.0 中文版安裝。
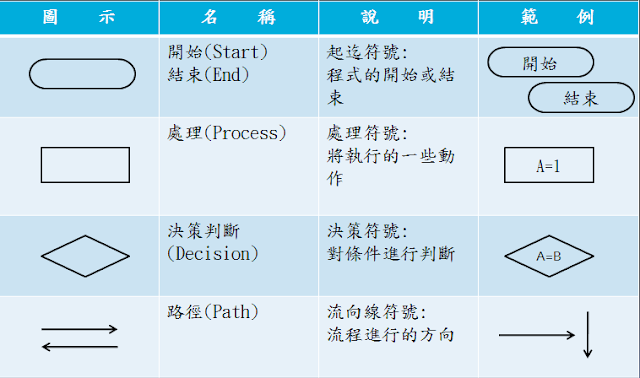
三、用電腦解題-程式流程圖(PPT)。
四、用電腦解題-最小公倍數。
五、最大公因數和最小公倍數題目教材。
六、Computational Thinking。
七、設計有關坐標計算的題目,並且使用電腦幫助解題。
題目:設計可以接收所輸入的答案,並在直角坐標平面上顥示出來。
2. 柯南以偵探徽章告訴偵探少年隊的成員他的位置,他要步美向右移動 4 個單位,光彥向左移動 8 個單位,元太向右移動 11 個單位,灰原向左移動 10 個單位,則偵探少年隊的成員可以全部與柯南集合在一起;若柯南所在位置坐標為-5,則其他成員原來位置的坐標所代表的數之和為【 】。
3. 計算〔4×(-3)-5×(-4)+73〕÷(13-40)=【 】。
注意:請只用Scratch所提供的標準積木進行設計,謝謝。
Scrtch 程式設計流程:
1.
Computational
Thinking。
A.
分解問題。
B.
找出規律。
C.
歸納與抽象化。
D.
設計演算法。
I.
有限性。
II. 明確性。
III.有效性。
IV. 輸入資料。
V.
輸出資料。
2.
設計流程圖。
A.
循序結構。
B.
選擇結構。
I.
是否選。
II. 二選一。
III.多選一。
C.
重覆結構。
I.
前測式。
II. 後測式。
3.
撰寫程式碼。
I.
序列(Sequence)。
II. 廻圈(Loops)。
III.平行(Parallelism)。
IV. 事件(Events)。
V.
條件(Conditionals)。
VI. 運算子(Operators)。
VII.資料結構(Data structure)。
VIII.
程式碼沒有一定標準,只要能解決上述問題即可。
4.
測試與除錯。
I.
編譯(Compile)。
II. 執行(Exeute)。
III.除錯(Debug)。
IV. 測試(Test)。
留言
張貼留言